Leet Code 560. Subarray Sum Equals K — Explained Python3 Solution

-


Image for post
Photo by Paweł Czerwiński on Unsplash

Problem Description

Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
Input:nums = [2,2,3,0,4,-1,1,6], k = 7
Output: 3

Solution

Obvious Solution

There is certainly a brute force way. Iterarte the whole list, check the sum of (currentElement to currentElement+1), (currentElement to currentElement + 2), pesudo code looks like:
Image for post

In total, there are 3 loops and make the time complexity O(N³). It should work but definitely not an efficient way. There are ways to optimize this since there are many duplication of computation and the complexity can be decreased to O(N²).

Best Solution (to me)

Obviously, each subarray will end up with some index. Let me use i to represent that some index. And sum(0 to i) is very easy (and cheap — just take O(N)) to get.
Look at below example at i = 4, sum(0 to 4)= X + K. That means sum(0 to 4) can be broken to 2 parts, the second part is what I desire(with the sum of K), the first part X is actaully another sum which accumulate from 0 to 1. Now there is some light: if I have sum(0 to i), I can assume there is an index j (where j<i) , check if sum(0 to i) - K occurs in previous sum(0 to 0), sum(0 to 1), sum(0 to 2)…sum(0 to i-1), and increase the counter when an occurance is found. The value of the counter is the number of subarrays ending with index i that qualify the sume of K. In below example for index = 4, only sum(0 to 1) + K = sum(0 to 4), then there is only 1 qualified subarray which is [3,0,4].
Image for post
Leet Code 560. Subarray Sum Equals K Ilustation

Please note that in some case, there could be more than 1 qualified subarray.
Again look into another example as followed. For subarrays that ending at index 5, there are 2 cases:
sum(0 to 2) + sum(3 to 5)
sum(0 to 1) + sum(2 to 5)
And sum(0 to 2) and sum(0 to 1) are equal (both to 0).

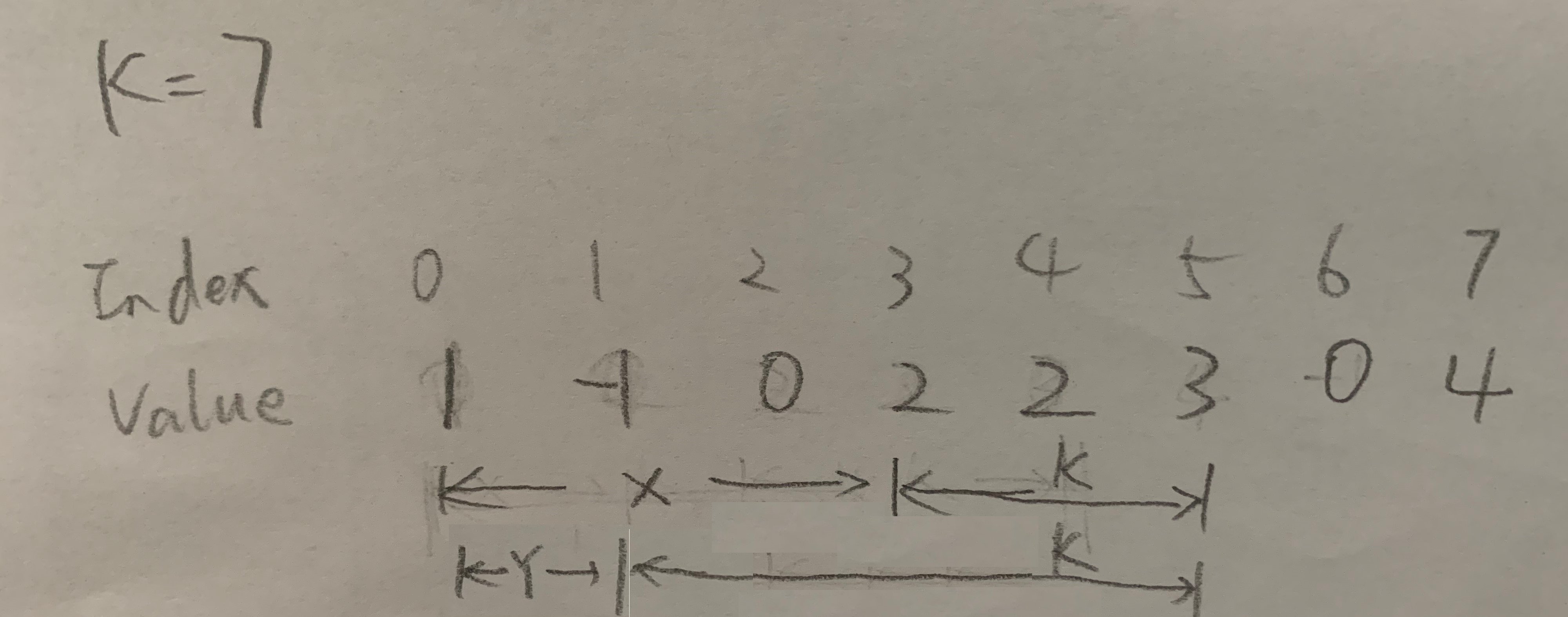
Image for post

Therefore, I need a Hashmap to record all sum(0 to x) (as the key) and its occurance (as the value). When I have sum(0 to i), I can check in the hasmap the value of sum(0 to i)-K to get the occurance number, and that number will the subarrays that ending with index i.
There is one trick however, again with my first example, what if sum(0 to i) itself is already equal to K like below the qualified subarray [2,2,3]? At this moment, the breakdown is : sum(0 to 2) = 0 + sum(0 to 2). The trick I play is add {0:1} to the hashmap saying for sum of 0, there is by default 1 occurance.

Image for post
Leet Code 560. Subarray Sum Equals K Ilustation

Alright, now here comes the code.

Time & Space Complexity
As above illustration/code shows, the time complexity is O(N): it just goes through each element in the input array for once only and with the loop each operation is O(1).
When it comes to space complexity: there is a hashmap which can scale (in worse case) with the size of input array, so it can take up to O(N) space and hence the space complexity is O(N).

Python 3 knowledge points

Within the solution, hashmap is used. I put together a post Python Cheatsheet with a section hashmap. Click https://medium.com/@edward.zhou/python3-cheatsheet-continuously-updated-66d652115549 to view more cheats :)

Extended Reading/Thinking

What if you are asked to return all subarrays?

Comments

Post a Comment

Popular posts from this blog

Leet Code 1060. Missing Element in Sorted Array — Explained Python3 Solution

-
Image
Problem Description Given a sorted array  A  of  unique  numbers, find the  K -th  missing number starting from the leftmost number of the array.   Example 1: Input: A = [4,7,9,10] , K = 1 Output: 5 Explanation: The first missing number is 5. Example 2: Input: A = [4,7,9,10] , K = 3 Output: 8 Explanation: The missing numbers are [5,6,8,...], hence the third missing number is 8. Solution Seeing the word " sorted " reminds me that there must be some trick to play with. One common thought of mine is binary lookup , which is used for quickly, in O(logN), to locate a specific element. And it turns out similar thoughts applies to this problem as well. Before getting to that, let me explain the brute force way a little bit. First I need to set a counter to count missing number I find as of now, in the beginning, it will be 0 for sure. Then I can certainly iterate the numbers one by one, the moment I get to index i, I will check if A[i] is the last element, if yes, then the miss
Read more

Leet Code 84. Largest Rectangle in Histogram — Graphically Explained Python3 Solution

-
Image
  Photo by  Pablo Hermoso  on  Unsplash Problem Description Given  n  non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram. Above is a histogram where width of each bar is 1, given height =  [2,1,5,6,2,3] . The largest rectangle is shown in the shaded area, which has area =  10  unit. Example: Input: [2,1,5,6,2,3] Output: 10 Solution Obvious Solution The obvious (and brute force) way is to use 2 pointers: left and right. Let left points to index 0 ~ N-1 and then right to left and N-1. For each left and right pair, I can calculate the area[left, right] using (right-left+1) * min(heights[left], heights[left+1],heights[left+2],…,heights[right]). Its time complexity is at least be O(N²). Best Solution (to me) [Credit]  This is described by @ TravellingSalesman  in disucssion area ( https://leetcode.com/problems/largest-rectangle-in-histogram/solution/ ) and here I just try to illustrate it furt
Read more

LeetCode 23. Merge k Sorted Lists— Graphically Explained Python3 Solution

-
Image
  Problem Description You are given an array of  k  linked-lists  lists , each linked-list is sorted in ascending order. Merge all the linked-lists into one sorted linked-list and return it. Example: Input: lists = [[1,1,5],[1,3,4],[2,6]] Output: [1,1,1,2,3,4,5,6] Explanation: The linked-lists are: [ 1->1->5, 1->3->4, 2->6 ] merging them into one sorted list: 1->1->1->2->3->4->5->6 Solution Obvious Solution The obvious (and brute force) way is to navigate ALL list items, save them into an array and then sort. The time complexity is: O(kN + kNLog(kN)) since for for total k Lists (each one with average N elements), I need to visit them all and the quick sort on final array takes kNLog(kN). The space complexity is O(kN) as all values will be saved. Best Solution (to me) Since each list is already sorted, I can definitely leverage that. To start with, let me use this example: To show it more clearer, let me put some twists (showing only the left
Read more