Leet Code 1155. Number of Dice Rolls With Target Sum — Graphical Explained Python3 Solution

 

Problem Description

You have d dice, and each die has f faces numbered 1, 2, ..., f.

Return the number of possible ways (out of fd total ways) modulo 10^9 + 7 to roll the dice so the sum of the face up numbers equals target.

Example 1:

Input: d = 1, f = 6, target = 3
Output: 1
Explanation: 
You throw one die with 6 faces.  There is only one way to get a sum of 3.

Example 2:

Input: d = 2, f = 6, target = 7
Output: 6
Explanation: 
You throw two dice, each with 6 faces.  There are 6 ways to get a sum of 7:
1+6, 2+5, 3+4, 4+3, 5+2, 6+1.

Example 3:

Input: d = 2, f = 5, target = 10
Output: 1
Explanation: 
You throw two dice, each with 5 faces.  There is only one way to get a sum of 10: 5+5.

Example 4:

Input: d = 1, f = 2, target = 3
Output: 0
Explanation: 
You throw one die with 2 faces.  There is no way to get a sum of 3.

Example 5:

Input: d = 30, f = 30, target = 500
Output: 222616187
Explanation: 
The answer must be returned modulo 10^9 + 7.

Solution

Obvious Solution

The ituition is that this problem can be divided and conquered in small sub problems. Take an example of d = 2, f = 5, target = 10, assuming I’m going to roll the second die, since its value can only be 1,2,3,4,5, I only need to know possibilities of the previous die (the first one) being 9,8,7,6,5 and then add up those possibilities. Obviously, the possibilities of the previous die being 9,8,7,6,5 is 0,0,0,0,1. Therefore, only 0+0+0+0+1=1 way to get to the target 10.

Using a little math to help generalize the formula:

Ways(d, target) = Ways(d-1, target-1) + Ways(d-1, target-2) + … …+ Ways(d-1, target-f)

In short, the number of ways of current die is decided by its previous die’s ways to compose some (smaller) targets.

Certainly, there will be details to handle, for example, target-x needs to be postive. But with that understanding in mind, it will be relatively easy to write down below codes.

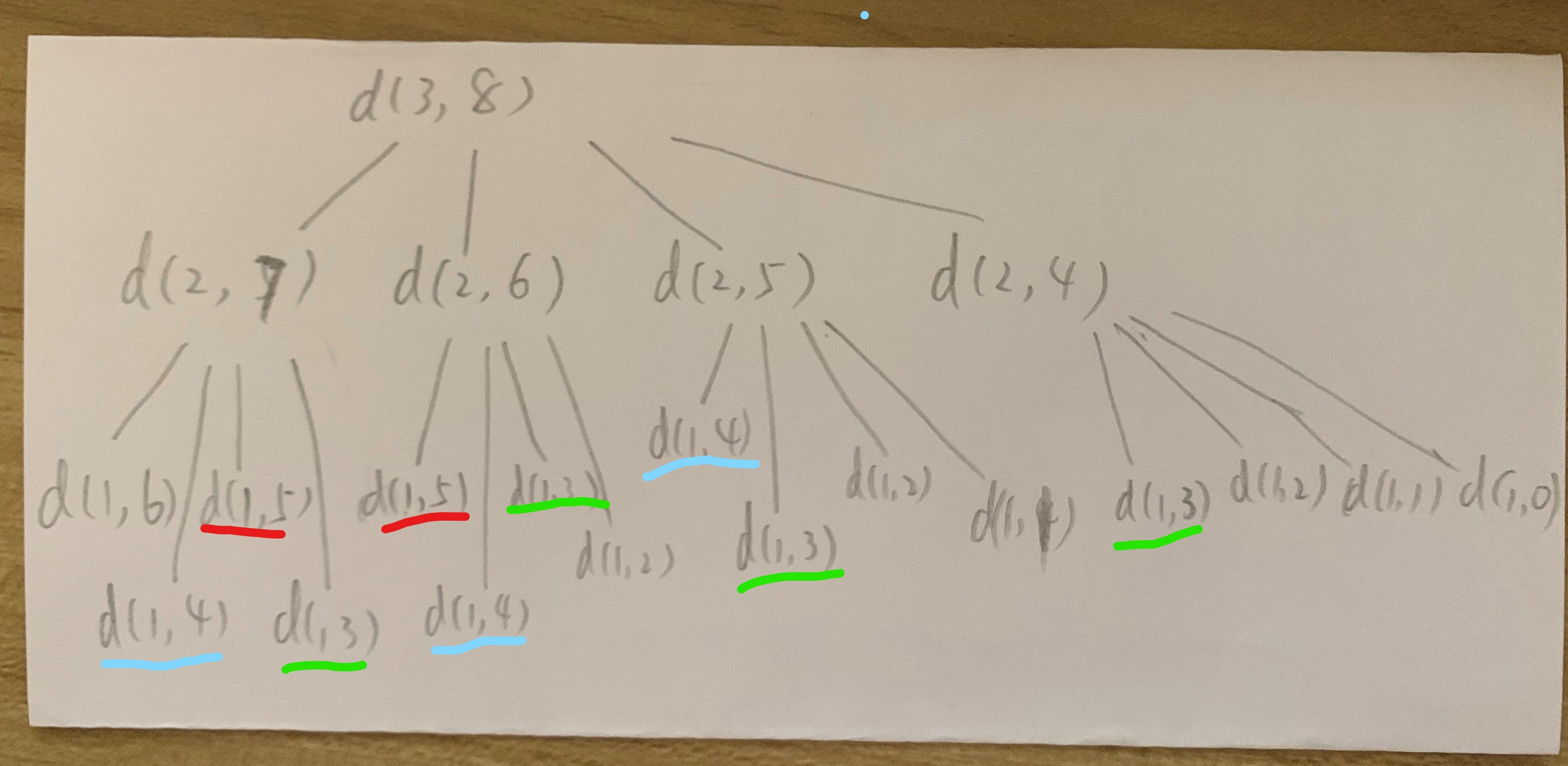
Please note that there is a cache mechanism which will help to avoid TLE (Time Limit Exeeded )in LeetCode. I use another example where d=3, f=4, target=8 to illustrate the necessity of cache in below graph. As show d(3,8) = d(2,7)+d(2,6)+d(2,5)+d(2,4) and then d(2,7),d(2,6),d(2,5),d(2,4) can each be broken into d(1,x) where the repeated pairs appear. Like d(1,4) actually contribute to d(2,7), d(2,6) and d(2,5). Caching the result for d(1,4) can allow reduce the time for recalculation of it.

The codes are available here. Although this solution can beat 68.09% Python3 solutions, which is not outstanding because it’s using recursive calls (which introduces stack and brings time costs for entering/exiting functions). There is actually a more lightweight solution in second part of this article.

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int):        
        modulo = 10**9 + 7
        cache = {}
        
        def numRollsToTargetHelper(dd, tt):
            if cache.get((dd,tt)) != None:
                return cache[(dd,tt)]
            nonlocal f
            if dd == 1:
                if tt <= f:
                    return 1
                else:
                    return 0
            
            ret = 0
            for i in range(1, f+1):
                if tt - i > 0:
                    ret += numRollsToTargetHelper(dd-1, tt-i)
            cache[(dd,tt)] = ret
            return ret
        
        ret = numRollsToTargetHelper(d, target)
        return ret % modulo

Best Solution (to me)

When looking at above graph which illustrates how to divide and conquer the problem, it’s very natural to think using DP (Dynamic Programming). My understanding of the core of DP is to break down a problem to the same problem with smaller volume sizes in each dimesion.

Revisit below formula, it’s actually a promising DP equation itself :)

Ways(d, target) = Ways(d-1, target-1) + Ways(d-1, target-2) + … …+ Ways(d-1, target-f)

However, DP is notorious for its uneasy to consume and I myself is pretty struggling sometimes. I will try to explain it as clear as possible, however, whenever confused, it might be a good idea for one to revisit the above grahp (and the following one as well).

I will continue using the example of d=3, f=4, target=8. Assuming if there is only 1 die, apparently, for target =1,2,3,4,5 the corresponding way is 1,1,1,1,0. Actually here I calculate d(1,1), d(1,2),d(1,3),d(1,4),d(1,5). Specifically, d(1,5)=0 means there is no way to roll a die with 4 faces (1,2,3,4) that can produce a target 5. Now look at the second line, d(2,1) should be 0 as well (in the graph, it’s ‘X’) meaning with 2 dice, it’s impossible to get a target of 1. And d(2,2) = d(1,1) , d(2,3) =d(1,1)+d(1,2), for the RED circle one d(2,6)=d(1,2) +d(1,3) + d(1,4) + d(1,5) while for the GREEN cirle one d(3,8)=d(2,7) +d(2,6) + d(2,5) + d(2,4)=12 and that means for 3 dices(each with 4 faces) to get a sum(target) of 8, there are 12 ways!

Final source code is available in below:

Time & Space Complexity

By checking above graph in DP solution, the time complexity is O(d*target*f): there are total d*target grids’ values to calculate, while for each value, I need to add f numbers (from previous line). Its space complexity is O(d*target), which can be improved to be O(target) since each line grid is only related to previous line and it’s actually a slide window (from right to left).

Since DP is actually another type of recursive calls (but saving function calls), recursive way is also O(d*target*f). And its space complexity is O(d*target).

Python 3 knowledge points

1, Cache decorator

Besides using a customized cache in recursive way, there is a decorator name lru_cache which I can add before a function definition. Therefore, I can save some lines to make a neat version like below.

class Solution:
    def numRollsToTarget(self, d: int, f: int, target: int):        
        modulo = 10**9 + 7        @lru_cache(max_size=10000)
        def numRollsToTargetHelper(dd, tt):
            nonlocal f
            if dd == 1:
                if tt <= f:
                    return 1
                else:
                    return 0
            
            ret = 0
            for i in range(1, f+1):
                if tt - i > 0:
                    ret += numRollsToTargetHelper(dd-1, tt-i)
            return ret
        
        ret = numRollsToTargetHelper(d, target)
        return ret % modulo

2, Initialize a matrix

Unlike C++ or Java, Python3 is not that handy to create a matrix (a list of list). Below code can help to create a d lines matrix while each line contains target number of elements.

dp = [[0 for i in range(target+1)] for j in range(d+1)]

Please note that below code looks correct but it is actaully dangerous.

dp = [[0] * target] * d

An exmaple to reveal the danger: although I only set dp[0][1] to 1, behind the scene, dp[1][1] is also changed! The reason behind that is [[0] * target] * 2 means replicate a list object as 2 copies, so both lines refer to the same list object!

>>> target=2
>>> d=2
>>> dp=[[0] * target] * d
>>> dp
[[0, 0], [0, 0]]
>>> dp[0][1] =1
>>> dp
[[0, 1], [0, 1]]

Extended Reading

Python3 cheatsheet:

https://medium.com/@edward.zhou/python3-cheatsheet-continuously-updated-66d652115549