Leetcode 1551. Minimum Operations to Make Array Equal— Graphically Explained Python3 Solution

-

Problem Description

In one operation, you can select two indices x and y where 0 <= x, y < n and subtract 1 from arr[x] and add 1 to arr[y] (i.e. perform arr[x] -=1 and arr[y] += 1). The goal is to make all the elements of the array equal. It is guaranteed that all the elements of the array can be made equal using some operations.

Given an integer n, the length of the array. Return the minimum number of operations needed to make all the elements of arr equal.

Example 1:

Input: n = 4
Output: 4
Explanation: arr = [1, 3, 5, 7]
First 3 operations choose x = 3 and y = 0, this leads arr to be [4, 3, 5, 4]
Now take 1 operation choose x = 2 and y = 1, thus arr = [4, 4, 4, 4].

Example 2:

Input: n = 7
Output: 12

Solution

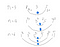
To start with, just use a simple example like [1,3,5] (where n=3).

As the below picture shows, when n=3, the quickest way to make all elements equal is to

  1. increase array[0] by 1 and decrease array[2] by 1
  2. repeat #1

So the minimum operation is 2. This is not strict prove and the philosophy behind is to make all values increase/decrease towards the median value since, in each operation, I will have one value increase by 1 and the other decrease by 1, it will be natural to do that against mirrored elements in each end.

Now, look at other examples shown above like n=4 and 6. Mirrored elements will be taken by operations in X times where X=1,3,5,…, n/2 if n % 2 == 0. For n % 2 ==1, X will be 2,4,6,…,n-1.

OK, so the number of operations is the sum of an array

1,3,5,…, n/2 if n % 2 == 0

2,4,6,…,n-1 if n % 2 == 1

This is basically a math question now. The sum of an array like below is (start + end) * size_of_array / 2 = (start + start + size_of_array * 2–2) * size_of_array / 2 = (start + size_of_array -1) * size_of_array

start, start +2, start +4, …, end

Translating above illustration will lead to:


Time & Space Complexity

Space complexity will be O(1) as well since no extra space(like an auxiliary array) is used.

Extended Reading

https://medium.com/@edward.zhou/python3-cheatsheet-continuously-updated-66d652115549

Comments

Post a Comment

Popular posts from this blog

Leet Code 1060. Missing Element in Sorted Array — Explained Python3 Solution

-
Image
Problem Description Given a sorted array  A  of  unique  numbers, find the  K -th  missing number starting from the leftmost number of the array.   Example 1: Input: A = [4,7,9,10] , K = 1 Output: 5 Explanation: The first missing number is 5. Example 2: Input: A = [4,7,9,10] , K = 3 Output: 8 Explanation: The missing numbers are [5,6,8,...], hence the third missing number is 8. Solution Seeing the word " sorted " reminds me that there must be some trick to play with. One common thought of mine is binary lookup , which is used for quickly, in O(logN), to locate a specific element. And it turns out similar thoughts applies to this problem as well. Before getting to that, let me explain the brute force way a little bit. First I need to set a counter to count missing number I find as of now, in the beginning, it will be 0 for sure. Then I can certainly iterate the numbers one by one, the moment I get to index i, I will check if A[i] is the last element, if yes, then the miss
Read more

Leet Code 84. Largest Rectangle in Histogram — Graphically Explained Python3 Solution

-
Image
  Photo by  Pablo Hermoso  on  Unsplash Problem Description Given  n  non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram. Above is a histogram where width of each bar is 1, given height =  [2,1,5,6,2,3] . The largest rectangle is shown in the shaded area, which has area =  10  unit. Example: Input: [2,1,5,6,2,3] Output: 10 Solution Obvious Solution The obvious (and brute force) way is to use 2 pointers: left and right. Let left points to index 0 ~ N-1 and then right to left and N-1. For each left and right pair, I can calculate the area[left, right] using (right-left+1) * min(heights[left], heights[left+1],heights[left+2],…,heights[right]). Its time complexity is at least be O(N²). Best Solution (to me) [Credit]  This is described by @ TravellingSalesman  in disucssion area ( https://leetcode.com/problems/largest-rectangle-in-histogram/solution/ ) and here I just try to illustrate it furt
Read more

LeetCode 23. Merge k Sorted Lists— Graphically Explained Python3 Solution

-
Image
  Problem Description You are given an array of  k  linked-lists  lists , each linked-list is sorted in ascending order. Merge all the linked-lists into one sorted linked-list and return it. Example: Input: lists = [[1,1,5],[1,3,4],[2,6]] Output: [1,1,1,2,3,4,5,6] Explanation: The linked-lists are: [ 1->1->5, 1->3->4, 2->6 ] merging them into one sorted list: 1->1->1->2->3->4->5->6 Solution Obvious Solution The obvious (and brute force) way is to navigate ALL list items, save them into an array and then sort. The time complexity is: O(kN + kNLog(kN)) since for for total k Lists (each one with average N elements), I need to visit them all and the quick sort on final array takes kNLog(kN). The space complexity is O(kN) as all values will be saved. Best Solution (to me) Since each list is already sorted, I can definitely leverage that. To start with, let me use this example: To show it more clearer, let me put some twists (showing only the left
Read more